R语言初步——数据处理、绘图与编程

R语言初步——数据处理、绘图与编程

本文介绍的是一套幻灯片，共包括120张，较为详细的介绍了R语言，以及简单统计分析的实现，包括方差分析、回归，以及绘图、编写函数的方法。

内容如下：

  • 一、R简介
  • 二、函数与对象
  • 三、脚本编程
  • 四、R绘图
  • 五、编写函数
  • 六、数据保存
    以下是幻灯片的内容，希望对感兴趣的读者能有促进作用。

幻灯片下载:

R语言初步 统计绘图与编程.ppt

用R高清绘图:分辨率600DPI

用tiff命令可以生成指定分辨率的tiff格式的图片,tiff一般很大, 所以一般都进行压缩, 常用如 lzw压缩.

1
2
3
tiff(file = "C:/test1.tiff", res = 600, width = 4800, height = 4800, compression = "lzw")
plot(1:22, pch = 1:22, cex = 1:3, col = 1:5)
dev.off()

Phylomatic生成进化树及物种功能性状聚类

Generating phylogenetic trees with Phylomatic and dendrograms of functional traits in R

基于现有的物种之间的进化关系，将其拟合成一个进化树，一直是进化生物学家和生态学家非常关心的问题。Phylomatic软件使得用户可以用物种名录生成基于APGIII的进化树框架，进而用Phylocom软件拟合出分化时间。这使得计算群落内部和群落之间的系统发育关系成为可能。

同系统发育关系类似，物种在的功能性状组成的多维空间中的距离，对于回答诸如群落物种组成的关系也是极为重要的。

这里的幻灯片是2010年8月在Community phylogenetics 培训班上的资料。内容第一部分涉及如何在Phylomatic上生成进化树，怎样在Phylocom中校对枝长。第二部分为如何根据物种的功能性状，推测物种之间的距离，并进一步用聚类分析的方法给出聚类结果。如何对结果进行筛选等。

供有兴趣的同仁参考。

下载 幻灯片 Generating phylogenetic trees with Phylomatic

[转载]何芳良教授谈生态学论文的写作与发表

注： 以下内容全为转载

读过何老师在台湾福山植物园与同学和部分老师关于撰写论文和投稿的对话之后，觉得很有启发。在征得何老师同意后，将全文贴于此，希望对大家有所帮助。 

何芳良老师谈生态科学写作与发表 (台湾福山植植物园, August , 2007) 

  1. 学员问： 以老师的经验，如果您收到的稿件您一看就会退稿，通常这些稿件会有什么错误? 

何老师答： 看不同的杂志，例如Ecology Letters，Impact factor 7.6，退稿率是60%，只有40%能送出去review，而这之中还有一半会被拒绝接受，最后只有百分之十几可以被接受，所以这个期刊拒稿率是很高的，所以如果你有paper投到Ecology Letters被拒了，Don’t feel bad. 不是因为你的研究不好，而仅仅是该期刊当年只能刊登有限数目的文章。Ecology拒稿率也很高，来稿中有40%~50%我们不送出去审查。至于Plant Ecology，该期刊比较一般，大部分文章都会送出去审。但有的稿子读了会令人头痛，作者自己都搞不清楚自己在写什么。这样的的稿子一定不会送审。那大家写文章，很难讲怎样的文章可以被接收或被拒绝，但是有一个基本的通则，因为科学研究的根本目的就是在 “advance knowledge”，你的knowledge有可能是local knowledge就是有local impact，有的knowledge有global impact，这个没有关系，但是一篇文章一定要是一个「complete story」，就是一个能自圆其说的有主题的完整故事，这个故事可大可小但一定要完整，不能有缺口。首先你要先问自己，你做的问题，是不是能给读者带来新的knowledge，新的ideas，新的东西，这个非常重要！ 

我们大家都知道，写文章最最关键的地方就是Introduction，那是文章的灵魂，如果Introduction写的不好，你后面的东西即使作的很好，也已经将自己处于劣势，并不是说你的文章会被拒，但will not be favored。所以Introduction一定要写好。我到现在有时候写文章，一个星期写一个 Introduction，就是每一个字，每一句话都要仔细推敲，为什么要写这个句子，都要有理由，也就是逻辑很重要。 

从科学的角度来讲，写文章的时候，尽量，尽量要「make a hypothesis」，就是很清楚的说明，我的研究是要测试这个假说，而这个hypothesis是什么要说明白。这样就可以让自己的文章处于优势。甚至你的文章真正作的东西是描述性的, 即描述某某现象，但最好不要这么写，就是同样的意思也尽量改写成「我的研究是要测试某个假说…」，这样就可以获得优势。虽然不能保证你的文章会被接受，但reviewers和editor会喜欢这样的说法。你的目的可以是description，但是make some hypotheses, make something interesting。虽然你的目的是描述，但我想你总能够找出一两点东西出来test。你假如说我的paper的目的是描述例如vegetation composition, distribution, etc. That doesn’t work! 很少有期刊会愿意发表描述性的文章。 

然后，当然你的文章要有很好的question、很好的idea、solid data还有分析方法越fancy越好，这个很重要。例如说你做一个简单的regression，如果是传统的regression，这样不会让别人很excited，但是如果你能加进去一点空间的东西，很容易提升文章的品质，或是使用一些新发展的分析方法都可以增强自己文章的竞争力。 

另外，Don’t write a big paper. Write a small paper。就是针对一个问题。把这个问题说清楚了，就是make a complete story。我举我自己的一个例子，胡新生和我有一篇paper在Ecology Letters，另外一篇在American Naturalist in press，这两篇原来是一篇paper，我们原先是送到Ecology Letters，被送审了，但其中有一个reviewer，他是不对的，他原来是作物理的，我们的文章里有一个公式推导，但那个reviewer总是认为我们的公式不对，但真正来讲我们的公式是对的，是他误解了，但就由于这点，Ecology Letters把我们的文章拒绝了。后来我们把这篇文章分成两篇，一篇送到Ecology Letters，很快就被接受了，另外一篇我们送到American Naturalist。所以你就是不要去研究一个很大的问题，只要make a complete story。尽管我们送去Ecology Letters的文章较短(five journal pages)，但确实是一个 complete story，一个interesting story。所以你的文章不要写得很大，很多东西，不要放进去很多ideas，很多points。一篇paper只要有一个interesting point，为了这个point去make a complete story，这样就可以了。假如写了很多东西放在一起反而不好。 
拒稿是很平常的一件事，我们已经被打的遍体鳞伤、麻木不仁了… 

  1. 学员问：例如Ecology Letters有一个很重要的特色就是其decision time只有二十几天而已，那他们是把那60%没有送出去的稿件的decision time都给加进去吗? 

何老师答： 不是这样的，该期刊不管你的稿件是被拒绝还是送审，六个星期一定会告诉你结果。所以主编会把我们编辑逼的很紧，时限到了如果主编没有收到编辑们的答复，就会自己下决定了，但这种情况很少发生。 

  1. 学员问： 请问老师，平均来说，你一篇paper最后被接收前会被拒绝几次? 

何老师答： 看情况，有的paper运气好很快就被接受，有的paper运气不好例如投两次，像我投过三次，我至少有两篇很重要的papers投过两次。例如我1996年投在American Naturalist的paper，事实上是我到目前为止最喜欢的一篇paper（种面积曲线），当初因为不敢投到太好的期刊，所以就投到Ecology，结果编辑并没有将我的稿件送出去审，反而建议我将稿件投到theoretical journal 或是 forest journal，这个就自相矛盾，他可能看到我的单位是Canadian Forest Service。所以我跟你们讲，当你们的稿件被拒绝的时候，不要觉得自己的稿件bad，要去看编辑提供的意见，要去抓住很不合理的意见，你假如有足够的信心，你觉得自己的paper很好，你可以去向主编抗辩。后来我们向Ecology主编讲，这样的决定是不合理的，所以主编让我们再submit一次，然后请另外一个editor来裁决，但是在我们收到这个裁决前一天，我们已经将稿件送到American Naturalist，而且很快就被接受了，我们被Ecology拒绝最后反而因祸得福，因为American Naturalist是比Ecology要好的期刊。所以我建议你们，当你们对自己的研究很有信心，Don’t give up. 你要很仔细的看编辑的review comments，然后可以向主编抗辩，You still have a chance! 

  1. 黄老师问： 发表文章的速度与品质何者为重? 我的经验是有时候想投去impact factor比较高的期刊，可是没有评估好就被拒绝了，或者修改后依然被拒绝，这样一来有时候就拖半年了。有时候投去impact factor低的期刊往往马上就被发表了。老师对这些取舍有何建议? 

何老师答： 我的建议是不要急。你假如写了一篇好的paper，你可以先搁着，例如两个星期。例如我经常碰到我的学生，他们文章写好了，觉得很完整了，然后就很想赶快送出去，事实上这样不好。因为你不会每天都有good idea，但当你有good idea的时候，你一定要争取机会，不要错失良机。例如我这篇paper写好了，但过两个月再看，就会觉得有的地方写得很可笑。所以不要急，文章写好了先放一边，暂时先把他忘了，等一两个星期再来看。 

我觉得要尽量争取好的journal，好的journal和坏的journal确实差别很大，不承认不行。例如在北美找工作，作ecology的，像Am. Nat.、Ecology Letters、Ecology、Ecological Monographs，你假如有这些paper，立刻人家就会觉得你很不错。假如你有的是Journal of Biogeography、Ecography，这些也是很不错的journal，但是在人家的心目中还是没办法和Am. Nat.这些journal比。所以你要是有一个很好的idea，尽量把他develop到你满意为止，然后Try the best you can。所以我的建议是从最好的journal开始试，不行再往下降。例如送到Ecology Letters，他们的审查意见一般来讲水平都是很高的，这些意见都是很fair，确实get to the point，所以可以让你知道你的问题在什么地方。所以不要被journal A拒绝了，什么也不作就直接送到journal B，你可能会得到相同的命运，你一定要修改。 

另外例如你有稿件送到Science或是Nature被拒绝了，你觉得是Good paper，你可以把所有的comments一起送到例如Ecology Letters，看他们要不要收。Ecology Letters encourages这样做。 

  1. 丁老师问： 想请教对时间管理有什么建议。 

何老师答： 是的，时间是一个big problem。像我自己做事比较认真，可以说非常认真，像写paper我是一丝不茍的，例如我的学生(甚至博士后)的文章拿过来给我修改，我几乎是每个字都给改了，完全地改过，意思是同一个意思。只要我觉得不满意或不能忍受，就会大大地修改。当然，这并非说我改的就一定更好，但是是我满意的。这就需要很多的时间，最好是学生能把manuscript写到完全满意后再送给老师修改，这样能节省很多时间。 

  1. 学员问： 老师请问你们决定reviewers的程序是怎样? 

何老师答： 很多journal 要求作者建议reviewers，这个要看不同的editors，懒一点的editors会按照你的建议去挑选reviewers，因为你已经提供了可能的reviewers，他只要click几下就可以把名单加到系统当中。如果是我的话，我一般都不会用你建议的reviewers，我会自己挑选。但假如你建议说有哪些人不应该审查你的文章，一般来讲我会接受你的请求，很多editor都会接受这样的要求。你假如觉得有哪位仁兄对你的文章一定会给负面的评论，你可以要求不要让他当reviewer，一般来讲editors都会尊重你的要求。 

  1. 学员问： 请问生态学的文章对于统计方法挑剔到什么程度? 我们需要真的很在意所有使用方法的假设吗？ 

何老师答： 回答是：Yes, 很在意。作统计分析的方法一定要对，而且解释一定要准确。你假如这些基本的东西都不对，那你的文章肯定没有机会被接受。有一点很重要，你的数据一定要满足你所用方法的条件。例如做线性回归，数据要独立，且要来自同一正态总体。(Anyway,所有统计方法都要求样本独立。) 尽管，在实际研究中，这些条件并不一定都能满足，但如果不注意，很容易被拒。因为这是拒稿最简单的理由，不费editor吹灰之力。再一例是，假如你有autocorrelation的东西，一定要把 autocorrelation考虑进去。我刚才讲了，最好能用fancy的分析方法，越fancy越好，当然，不要很复杂，不是peculiar or obscure的方法。如果你弄一个方法连编辑都看不懂就不好了。 

  1. 学员问： 请问英文写作上，什么是不可原谅的错误，就是编辑看到就不想继续看的? 

何老师答： 你假如有一些语法错误，没有问题，我们都可以理解。但是有一点很重要，逻辑，逻辑，逻辑，是非常非常重要的。你假如文章前言不搭后语，那就完蛋。刚才我说过，我写一个Introduction有时候要一个星期，我会每一句话都推敲。你说这句话，为什么要写这句话，所以逻辑非常重要。另外我还有一个advice就是use simple sentences，不要写很长的句子，as simple as possible，这个非常重要，尤其是我们这种英文不是母语的人。例如Ecology有一个category，就是对英语不是母语的人，假如paper还是不错的话呢，editor愿意为你修改，当然不要充满错误。英语不应该是一个major barrier ，但你应该照我刚才所说的使用简单的句子，尽量不要犯语法的错误。逻辑是最重要的，如果你没有逻辑的话，reviewer 会frustrated，这样你就没有机会了，他们根本不会看你的paper，有的reviewer甚至会告诉你，我就读到introduction，that’s it! 他的comment就是这么写的，那你的文章就被拒了。 

  1. 学员问： 假如我写了篇自认为很好的paper，如何去判断我的paper是不是有那样的品质去投到Science, Nature或是Ecology Letters，如何自己去作一个评断? 

何老师答： 这个就很难说，这个就要看你自己的感觉，如果你觉得你的文章是your best work，那就try the best journal，try the journal you wish to publish your work。你假如不试试看的话你永远没有机会。如果你的paper被拒绝了，Don’t feel bad! 被拒绝了并不是说你的paper不行，会有各种各样的原因。那些好的journal一年只能发表有限数量的paper，就是你的paper他觉得很不错，但跟其他的相比之下他们更愿意发表其他的，所以turn yours down，并不是说你的paper不行。 

  1. 学员问： 对于年轻的投稿者来说，他们在这个领域可能都没有reputation，reviewers和editors也不认识他们，然后地址感觉也是很奇怪的地址，会不会对他们的manuscript造成一些影响? 如果有的话影响又是什么? 

何老师答： 这个影响可能还是有一点，但你说是决定性因素呢，也不是。主要还是看你文章的品质，因为整体来讲这些editor的素养都较高，比较不会带有这些偏见。但是有一种倾向也是事实，有名的人稿子易被发表。这不奇怪，他们兼有两种优势(quality和reputation) 。即便如此，他们的稿子也常有被拒的。例如，Hubbell的中性理论投了很多地方，最终发表在1997的Coral Reefs上。这还是由于在那一年他被邀请在Coral Reefs的年会上做报告。依惯例Coral Reefs一定要发表年会上的报告，才不得不发表！ 

11.学员问： 老师刚才说到Introduction非常的重要，那我自己看paper的习惯是先看abstract和introduction，然后实验的部分我会看一下图表 ，然后直接跳到discussion。我想了解reviewer如果很忙的话，他们通常用什么样的顺序去看一篇paper？ 

何老师答： 他很忙的话就是看两部分，introduction 和method，因为method就包括了数据, result都不用看，因为你有method和introduction，你的result 通常能支持你的预期，discussion 就更不用看了。我说introduction很重要，但很多稿子被拒了是由于Methods。Introduction最重要，为什么呢? 读了Introduction就知道你这篇paper的水平。但是文章被拒稿了，原因最多的就是你的methods。例如你的paper还是不错的paper，但是不是很exciting，你的资料有spatial correlation，但是你的method里头没有考虑到，那个editor本来就想拒，这个就给editor很好的理由去拒绝你。很多editor都有很大的pressure去reject as many papers as they can。事实上这个paper把autocorrelation加进去是不困难的，但是你假如miss掉这个地方人家就不给你机会了。所以写文章不要rush，把这些漏洞都给补了，不让他们有这种拒绝你的机会。 

  1. 学员问： 关于使用图和表去表现我们的结果，通常我们在给一个talk的时候是比较喜欢用图，但不知道在文章上是不是也是这样? 

何老师答： 仍然是用图比较好，因为reviewer或读者通常不在乎确切的数字，因为ecology不是一个rocket science，因为你要把火箭发射到确切的地点，你的数字一点都不能错，否则的话就off your target miles away，但ecology不是rocket science，they don’t care 3.5 or 3.7。尽可能使用figure，不要使用table，没有人有那么多时间来推敲你的table。 

  1. 学员问： 研究题目的地域性影响会很大吗? 

何老师答： 有的问题，会有影响。写文章的时候最好避免针对local的东西去作大文章，最好是用local的数据来test某个假说，而且避免把local的名字放在文章的标题。但不是说有地域性的文章就发表不了，只要是你的研究确实advance knowledge，这个knowledge确实是new，有impact，有的journal还是愿意发表这些regional的paper。一般的建议还是尽量不要把有地域性的东西放在标题，不要一开始就让人感觉到你做的就只是福山的一个植被分析，那肯定journal的兴趣会减少几分。

如何绘制日食界限图？

日食界限图是表示日食可见区域的一种地图。包括日食的南北界限，日出日落时刻线，日出日落时初亏线，日出日落时复圆线。如2011年1月4日将发生一次日偏食，在欧洲大部分，非洲撒哈拉及其以北地区，中亚，西亚以及我国的西部可以见到日偏食。可见区域由若干条曲线围成。各曲线代表的含义分别为，

  • I， 日出时复圆。
  • II， 日出时食甚
  • III， 日出时初亏
  • IV， 日落时复圆
  • V， 日落时食甚
  • VI， 日落时初亏
    还有一条线段表示日食南界。在这个区域内部，可以见到日偏食的完整过程。区域之外则不可见。由于月亮自西向东运行，其速度远远超过太阳的向东运行的速度。因此，日食总是从西侧开始，在东侧结束。
    公元前2000年到公元3000年每一次日食kmz文件， 可以在 http://xjubier.free.fr/en/site_pages/SolarEclipsesGoogleEarth.html 下载。kmz文件可以被google earth读取。
    为了生成清晰度更高的日食界限图，笔者编写了相应的R函数，以绘制日食界限图。该函数基于maptools、mapproj、mapdata。使用前请先下载这三个程序包。
    由于绘制地图必须采用一定的投影方式，这里默认的投影方式为斜轴等面积投影。当然，高手可以通过阅读R的帮助信息，改变相应的地图投影方式，线段的颜色等，以达到满意的效果。
    图2 - 6
    plotkml绘制的日食界限图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
plotkml <- 
function(file, projection = "azequalarea" , parameter = NULL, grid = TRUE, info = TRUE,... ){
	 require(maptools)
     require(mapproj)
     require(mapdata)
    #match.arg(projection)
    zz <- getKMLcoordinates(file, ignoreAltitude = TRUE)
	x11(11,9)
    m <- map('world',proj= projection, parameter = parameter, orient=c(zz[[1]][2], zz[[1]][1], 0), ...)
    
	for(i in 1:length(zz)){                              ## Add lines to graph
	    if(is.data.frame(zz[[i]])){
		    if(ncol(zz[[i]]) > 3){
		        i = i + 1
            }		                                     ## Avoid  ncol > 3
		}
		
		if(is.list(zz[[i]])){
		    i = i + 1			                         ## Avoid  list > 3
		}
		
        if(is.vector(zz[[i]])){
            points(mapproject(list(y = zz[[i]][2], x= zz[[i]][1])), pch = "*", cex = 2, col = 2)
		}
		
		if(is.matrix(zz[[i]])){
            lines(mapproject(list(y = zz[[i]][,2], x= zz[[i]][,1])), col = "blue", ...)
        } 
		## print(i) used in debugging
    }
    
	if(grid){   ## Add map grid
        map.grid(m, lty = 1, col = "grey")
    }
	file1 <- readLines(file)
	
	if(title){ ## Add title
	    #file <- "c:/ASE_1800_04_24__4cdcf4f5330fb.kml"
        daterecord <- file1[grepl("when", file1)]
        date <- substring(gsub(" ", "", daterecord), 7, 16)
        type <- file1[grepl("Type:", file1)]
        stype <- gsub(" ", "", type)
        typesolar <- substring(stype, 12, regexpr("<br", stype) - 1)
        title(paste(typesolar, "solar eclipse on", date))
	}
	if(info){  ## Add details for this eclipse
	    ##UT
		## detail information
		bg <- which(grepl("<li>Magnitude:", file1))
		info <- file1[bg:(bg+4)]
		infosub <- gsub("</li>", "", gsub("&nbsp;","",gsub("<li>", "",gsub(" ", "", info))))
        text(-1.3, seq(1.4, 1.1, by = -0.1),infosub[1:4])
		
		## Partial Eclipse Begins
		bg <- min(which(grepl("<name>P1", file1)))
        sub <- file1[bg:(bg+100)]
        ind <- min(which(regexpr("<longitude>",sub)>0))
		info <- sub[c(ind, ind +1)]
		info1 <- gsub("de", "de:",gsub("/longitude","",gsub("/latitude", "", gsub("[<->]", "", gsub(" ", "",info)))))
		information <- c("Partial Eclipse begins:", info1)
		text(-1.3,seq(-1.1, -1.3, by = -0.1),information)
		
		## Partial Eclipse Ends
		bg <- min(which(grepl("last external", file1)))
        sub <- file1[bg:(bg+100)]
        ind <- min(which(regexpr("<longitude>",sub)>0))
		info <- sub[c(ind, ind +1)]
		info1 <- gsub("de", "de:",gsub("/longitude","",gsub("/latitude", "", gsub("[<->]", "", gsub(" ", "",info)))))
		information <- c("Partial Eclipse ends:", info1)
		text(1.3,seq(-1.1, -1.3, by = -0.1),information)
		
		## Greatest Eclipse Point
		bg <- min(which(grepl("Greatest Eclipse Point", file1)))
        sub <- file1[bg:(bg+100)]
        ind <- min(which(regexpr("<longitude>",sub)>0))
		info <- sub[c(ind, ind +1)]
		info1 <- gsub("de", "de:",gsub("/longitude","",gsub("/latitude", "", gsub("[<->]", "", gsub(" ", "",info)))))
		information <- c("Greatest Eclipse:", info1)
		text(1.3,seq(1.3, 1.1, by = -0.1),information)
	}
}

img
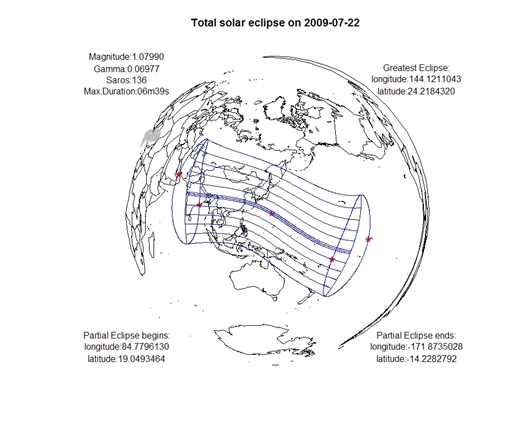
图2 2009年7月22日日全食路线图

img
图3 2020年6月21日日环食

img
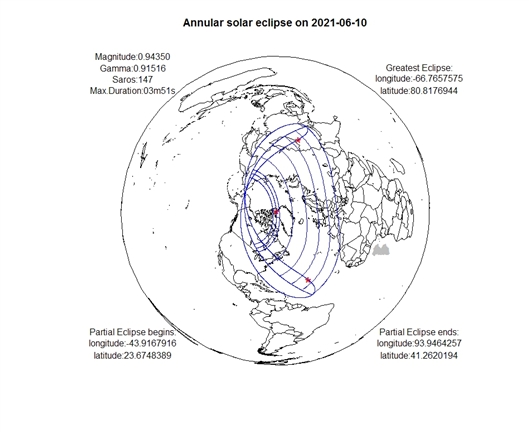
图4 2021年6月10日日环食

img
图5 2024年10月2日日环食

img
图6 2026年2月17日日环食

img
图7 2026年8月12日日全食

img
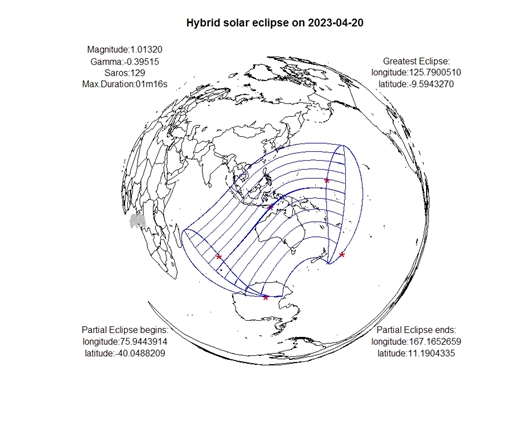
图8 2023年4月20日混合食（全环食）

img
图9 2035年9月2日日全食

img
图10 2024年4月20日日全食

如何计算日食的时间和类型（附R源代码）？

​ 日食的原理在小学课本中就有介绍，也就是月亮的影子遮挡住了太阳。日食每次必定发生在农历初一，因为农历初一是朔，此时从地心看起来月亮距离太阳最近。为什么要强调地心呢？ 因为在地球表面的不同位置，有视差的存在。天文学家在计算天象的时候，很多时候会先计算地心坐标。具体到某一个地点，再归算到地平坐标。

​ 日食的原理说来简单，但是计算起来并不容易。在我国古代，对日食的时间和类型的计算，是检验历法是否准确的重要标准。很多部历法由于不能准确的预测日月食，而不得不被新的历法所替代。如《新唐书.历志一》记载：“唐终始二百九十馀年，而历八改。初曰戊寅元历，曰麟德甲子元历，曰开元大衍历。”《新唐书.历志三上》又记载：”开元九年，麟德历署日蚀不效，诏僧一行作新历，推大衍数立术以应之…”。被誉为唐代历法首屈一指的《大衍历》，最后也难免被更为精确的历法所代替。

​ 这里采用的算法，是基于比利时天文学家Jean Meeus提出的现代天文算法。详情请参见许剑伟老师翻译的《天文算法》第52章。

​ 全部R程序改变自剑伟老师的《寿星万年历》javascript源代码。

### 快速日食搜索,jd为朔时间

### 改编自许剑伟老师的《寿星万年历》javascript源代码

### 输入儒略日2000，计算最近的朔的时间，并判断该次朔是否会发生日食。

DateSolarEclipse <-

function (jd){

​ rad = 180***3600/**pi; #每弧度的角秒数

​ radd = 180**/**pi; #每弧度的度数

​ pi2 = pi*****2;

​ pi_2 = pi**/**2;

​ J2000 = 2451545;

​

​ re**=list()**;

​ W = floor**((jd+8)/29.5306)*pi***2; #合朔时的日月黄经差

​ #合朔时间计算,2000前+-4000年误差1小时以内，+-2000年小于10分钟

​ t = ( W + 1.08472 **)/**7771.37714500204; #平朔时间

​ re**$jd = re$jdNewMoon = t***36525;

​ t2**=t***t

​ t3**=t2***t

​ t4**=t3***t;

​ L = ( 93.2720993**+483202.0175273***t**-0.0034029***t2**-t3/3526000+t4/**863310000 )/180*pi;

​ re**$ac=**1

​ re**$type=**’N’;

​ if**(abs(sin(L))>0.4)** return**(re)**; #一般大于21度已不可能

​ t = t - ( -0.0000331*tt + 0.10976 cos( 0.785 + 8328.6914*t)** **)/**7771;

​ t2**=** t*****t;

​ L = **(-1.084719 +7771.377145013*t **-0.0000331*t2 +

​ (22640 ***** cos(0.785+ 8328.6914*t +0.000152*t2)

​ +4586 ***** cos(0.19 + 7214.063*t -0.000218*t2**)**

​ +2370 ***** cos(2.54 + 15542.754*t -0.000070*t2**)**

​ + 769 ***** cos**(3.1 + 16657.383***t**)**

​ + 666 ***** cos**(1.5 + 628.302***t**)**

​ + 412 ***** cos**(4.8 + 16866.93***t**)**

​ + 212 ***** cos**(4.1 -1114.63*t)**

​ + 205 ***** cos**(0.2 + 6585.76***t**)**

​ + 192 ***** cos**(4.9 + 23871.45***t**)**

​ + 165 ***** cos**(2.6 + 14914.45***t**)**

​ + 147 ***** cos**(5.5 -7700.39*t)**

​ + 125 ***** cos**(0.5 + 7771.38***t**)**

​ + 109 ***** cos**(3.9 + 8956.99***t**)**

​ + 55 ***** cos**(5.6 -1324.18*t)**

​ + 45 ***** cos**(0.9 + 25195.62***t**)**

​ + 40 ***** cos**(3.8 -8538.24*t)**

​ + 38 ***** cos**(4.3 + 22756.82***t**)**

​ + 36 ***** cos**(5.5 + 24986.07***t**)**

​ -6893 ***** cos(4.669257+628.3076*t**)**

​ - 72 ***** cos**(4.6261 +1256.62*t)**

​ - 43 ***** cos**(2.67823 +628.31*t)***t

​ + 21**)** / rad**)**;

​ t = t + ( W - L ) / ( 7771.38

​ - 914 ***** sin**(** 0.7848 + 8328.691425t + 0.0001523t2 )

​ - 179 ***** sin**(** 2.543 +15542.7543*t )

​ - 160 ***** sin**(** 0.1874 + 7214.0629*****t ) );

​ re**$jd = re$jdNewMoon = jd = t***36525; #朔时刻

​ #纬 52,15 (角秒)

​ t2**=t***t**/**10000;

​ t3**=t2***t**/**10000;

​ mB**=** ( 18461cos(0.0571+ 8433.46616****t -0.640*t2 -1*t3**)**

​ + 1010***cos(**2.413 + 16762.1576 **t + 0.88 t2 + 25t3)*

​ + 1000***cos(**5.440 **-**104.7747 **t + 2.16 t2 + 26t3)*

​ + 624***cos(**0.915 + 7109.2881 **t + 0 t2 + 7t3)*

​ + 199***cos(**1.82 + 15647.529 *****t **-**2.8 *t2 -19*t3)

​ + 167***cos(**4.84 **-**1219.403 *****t **-**1.5 *t2 -18*t3)

​ + 117***cos(**4.17 + 23976.220 *****t -1.3 t2 + 6t3)

​ + 62***cos(**4.8 + 25090.849 **t + 2 t2 + 50t3)*

​ + 33***cos(**3.3 + 15437.980 **t + 2 t2 + 32t3)*

​ + 32***cos(**1.5 + 8223.917 **t + 4 t2 + 51t3)*

​ + 30***cos(**1.0 + 6480.986 **t + 0 t2 + 7t3)*

​ + 16***cos(**2.5 **-**9548.095 *****t **-**3 *t2 -43*t3)

​ + 15***cos(**0.2 + 32304.912 **t + 0 t2 + 31t3)*

​ + 12***cos(**4.0 + 7737.590 *t)

​ + 9***cos(**1.9 + 15019.227 *t)

​ + 8***cos(**5.4 + 8399.709 *t)

​ + 8***cos(**4.2 + 23347.918 *t)

​ + 7***cos(**4.9 **-**1847.705 *t)

​ + 7***cos(**3.8 **-**16133.856 *t)

​ + 7***cos(**2.7 + 14323.351 **t))*;

​ mB = mB / rad;

​ #月地距离 106, 23 (千米)

​ mR = **(**385001

​ +20905*cos**(5.4971+** 8328.691425t*+ 1.52 t2 + 25t3)**

​ + 3699cos(4.900 + 7214.06287t **-**2.18 *t2 -19*t3)

​ + 2956cos(0.972 + 15542.75429t -0.66 t2 + 6t3)

​ + 570***cos(**1.57 + 16657.3828 **t + 3.0 t2 + 50t3)*

​ + 246***cos(**5.69 **-**1114.6286 *****t **-**3.7 *t2 -44*t3)

​ + 205***cos(**1.02 + 14914.4523 *****t -1 t2 + 6t3)

​ + 171***cos(**3.33 + 23871.4457 **t + 1 t2 + 31t3)*

​ + 152***cos(**4.94 + 6585.761 *****t **-**2 *t2 -19*t3)

​ + 130***cos(**0.74 **-**7700.389 *****t **-**2 *t2 -25*t3)

​ + 109***cos(**5.20 + 7771.377 *t)

​ + 105***cos(**2.31 + 8956.993 **t + 1 t2 + 25t3)*

​ + 80***cos(**5.38 **-**8538.241 **t + 2.8 t2 + 26t3)*

​ + 49***cos(**6.24 + 628.302 *t)

​ + 35***cos(**2.7 + 22756.817 *****t **-**3 *t2 -13*t3)

​ + 31***cos(**4.1 + 16171.056 *****t -1 t2 + 6t3)

​ + 24***cos(**1.7 + 7842.365 *****t **-**2 *t2 -19*t3)

​ + 23***cos(**3.9 + 24986.074 **t + 5 t2 + 75t3)*

​ + 22***cos(**0.4 + 14428.126 *****t **-**4 *t2 -38*t3)

​ + 17***cos(**2.0 + 8399.679 **t))*;

​ mR = mR**/** 6378.1366;

​ t**=jd/**365250;

​ t2**=t***t;

​ t3**=t2***t;

​ #误0.0002AU

​ sR = **(**10001399 #日地距离

​ +167070*cos**(3.098464 + 6283.07585***t**)**

​ + 1396***cos(**3.0552 + 12566.1517 *t)

​ + 10302cos(1.10749 + 6283.07585t**)***t

​ + 172***cos(**1.064 + 12566.152 ***t)***t

​ + 436***cos(**5.785 + 6283.076 ***t)***t2

​ + 14***cos(**4.27 + 6283.08 *t)*t3)

​ sR = sR ***** 1.49597870691**/6378.1366***10;

​ #经纬速度

​ t**=jd/**36525;

​ vL = **(**7771 #月日黄经差速度

​ -914*sin**(0.785 + 8328.6914***t**)**

​ -179*sin**(2.543 +15542.7543*t)**

​ -160*sin**(0.187 + 7214.0629***t**))**;

​ vB = (-755*sin**(0.057 + 8433.4662***t**)** #月亮黄纬速度

​ - 82sin*(**2.413 +16762.1576*t));

​ vR =(-27299*sin**(5.497 + 8328.691425***t**)**

​ - 4184sin(4.900 + 7214.06287t**)**

​ - 7204sin*(**0.972 +15542.75429*t));

​ vL = vL**/**36525

​ vB = vB**/**36525

​ vR = vR**/**36525; #每日速度

​

​

​ gm = mRsin(mB)*vL/sqrt(vBvB**+vL***vL**)**;

​ smR**=** sR**-**mR; #gm伽马值,smR日月距

​ mk = 0.2725076;

​ sk = 109.1222;

​ f1 = (sk+mk)/smR; r1 = mk+f1*mR; #tanf1半影锥角, r1半影半径

​ f2 = (sk-mk)/smR; r2 = mk-f2*mR; #tanf2本影锥角, r2本影半径

​ b = 0.9972;

​ Agm = abs**(gm)**;

​ Ar2 = abs**(r2)**;

​ fh2 = mR**-mk/**f2;

​ if**(Agm < 1){**

​ h = sqrt**(1-gm***gm**)**

​ }else{

​ h = 0

​ }

​ ## h = Agm<1 ? sqrt(1-gm*gm) : 0; #fh2本影顶点的z坐标

​ ## ls1,ls2,ls3,ls4;

​ if**(fh2<h)** {

​ re**$**type = ‘T’; #全食

​ }else{

​ re**$**type = ‘A’; #环食

​ }

​

​ ls1 = Agm**-(b+**r1 );

​ if**(abs(ls1)<0.016)** re**$ac=**0; #无食分界

​ ls2 = Agm**-(b+Ar2)**;

​ if**(abs(ls2)<0.016)** re**$ac=**0; #偏食分界

​ ls3 = Agm**-(**b );

​ if**(abs(ls3)<0.016)** re**$ac=**0; #无中心食分界

​ ls4 = Agm**-(b-Ar2)**;

​ if**(abs(ls4)<0.016)** re**$ac=**0; #有中心食分界(但本影未全部进入)

​ if (ls1>0) {

​ re**$**type = ‘N’; #无日食

​ } else {

​ if**(ls2>0)** {

​ re**$**type = ‘P’; #偏食

​ } else {

​ if**(ls3>0)** {

​ re**$type = paste(re$type, ‘0’, sep = “”)**; #无中心

​ } else {

​ if**(ls4>0)** {

​ re**$type = paste(re$type, ‘1’, sep = “”)**; #有中心(本影未全部进入)

​ } else { #本影全进入

​ if**(abs(fh2-h)<0.019)** re**$ac=**0;

​ if**(** abs**(fh2)<**h ){

​ dr = vR***h/vL/**mR;

​ H1 = mR**-dr-mk/**f2; #入点影锥z坐标

​ H2 = mR**+dr-mk/**f2; #出点影锥z坐标

​ if**(H1>0)** re**$type=**’H3’; #环全全

​ if**(H2>0)** re**$type=**’H2’; #全全环

​ if**(H1>0&H2>0)** re**$type=**’H’; #环全环

​ if**(abs(H1)<0.019)** re**$ac=**0;

​ if**(abs(H2)<0.019)** re**$ac=**0;

​ }

​ }

​ }

​ }

​ }

​ return (re);

}

#取整数部分

int2 <-

function (v) {

return (floor(v));

}

### 公历转儒略日

JD <-

function**(y,m,d){**

n**=0;G=**0;

if**(y***372**+m***31**+int2(d)>=588829)**

​ G = 1; #判断是否为格里高利历日1582372+1031+15

if**(m<=2)** {

​ m = m **+**12;

​ y = y - 1;

}

if**(G > 0)** {

​ n**=int2(y/100)**;

​ n**=2-n+int2(n/4)**; #加百年闰

}

res <- int2**(365.25*(y+4716))** + int2**(30.6001*(m+1))+d+**n - 1524.5;

class**(res)** <- “JD”

return**(res)**

}

### 将儒略日转换为儒略日2000

JD2000 <-

function**(jd){**

res <- jd - JD**(2000,1,1)**

return**(res)**

}

### 将日期转换为儒略日2000

date2JD2000 <-

function**(y,m,d){**

​ juliand <- JD**(y,m,d)**

​ res <- JD2000**(juliand)**

​ return**(res)**

}

### 打印JD类型对象的方法

print.JD <-

function**(JD){**

​ print**(sprintf(“%f”,JD))**

}

##儒略日转为公历

Julian2Date <-

function**(jd){**

r = list**()**;

D = int2**(jd+0.5)**;

F**=** jd**+0.5-**D #取得日数的整数部份A及小数部分F

if**(D >= 2299161)** {

​ c = int2**((D-1867216.25)/36524.25)**;

​ D = D + 1 + c - int2**(c/4)**;

​ }

D = D + 1524;

r**$Y = int2((D - 122.1)/365.25)**;#年数

D = D - int2**(365.25***r**$Y)**;

r**$M = int2(D/30.601)**; #月数

D = D - int2**(30.601***r**$M)**;

r**$**D = D; #日数

if**(r$M>13)** {

​ r**$M = r$**M - 13;

​ r**$Y = r$**Y - 4715;

​ } else {

​ r**$M = r$**M - 1;

​ r**$Y = r$**Y - 4716;

​ }

#日的小数转为时分秒

F = F ***** 24;

r**$h=int2(F)**;

F = F - r**$**h;

F = F ***** 60;

r**$m=int2(F)**;

F = F **-r$**m;

F = F ***** 60;

r**$s=**F;

return**(r)**;

}

#日期转为字符串

DD2str <-

function**(r){**

Y = r**$**Y

M = r**$**M

D = r**$**D;

h = r**$**h;

m = r**$**m;

s = int2**(r$s+0.5)**;

if**(s >= 60)** {

​ s = s - 60;

​ m = m + 1;

​ }

​

if**(m >= 60)** {

​ m = m - 60

​ h = h + 1;

​ }

h = paste**(“0”, h, sep = “”)**;

m = paste**(“0”, m, sep = “”)**;

s = paste**(“0”, s, sep = “”)**;

Y = substr**(Y, nchar(Y)-** 4, nchar**(Y)** );

M = substr**(M, nchar(M)-** 1, nchar**(M)** );

D = substr**(D, nchar(D)-** 1, nchar**(D)** );

h = substr**(h, nchar(h)-** 1, nchar**(h)** );

m = substr**(m, nchar(m)-** 1, nchar**(m)** );

s = substr**(s, nchar(s)-** 1, nchar**(s)** );

res <- paste**(Y,”-“,M,”-“,D,” “,h,”:”,m,”:”,s, sep = “”)**;

return**(res)**

}

JD2str <-

function**(jd){** #JD转为串

r = DD**(** jd );

res <- DD2str**(** r );

return**(res)**

}

### 判断距离输入日期最近的朔，有没有日食发生。

## “P”为偏食

## “T”为全食

## “A”为日环食

## “N”没有日食发生

find.solar.eclipse <-

function**(y,m,d){**

​ res <- list**()**

​ dd <- DateSolarEclipse**(date2JD2000(y,m,d))**

​ date.solar.eclipse <- DD2str**(Julian2Date(dd$jdNewMoon + JD(2000,1,1)** + 0.5**))**

​ type <- dd**$**type

​ res**$**NewMoonTime <- date.solar.eclipse

​ res**$**EclipseType <- type

​ return**(res)**

}

##距离1987年9月23日最近的朔，以及日食类型

find.solar.eclipse**(1987,9,23)**

phylotools:处理DNA条码（DNA-Barcoding）序列的程序包

DNA条码，是利用聚合酶链式反应（PCR）及测序手段，将每个物种筛选出特定的一个或基因，共同组成的物种鉴定系统。DNA条形码在不同的类群中选取的基因不同，例如植物中常用的DNA条码相关的基因多为叶绿体中的基因，常包括rbcLa, matK, ITS, 5.8S, trnH-psbA等等，各基因的进化速率不同，互相参考，以便于对物种的准确鉴定。如果这一体系建立的比较精准，那么以后只需要对样品的相应基因进行PCR就可以实现对物种的准确鉴别。相比传统的依据物种形态的鉴别手段，应用的范围更加广泛。

然而DNA序列的fasta文件及比对之后的phylip文件处理是较为繁琐。特别是在处理测序后fasta文件中DNA序列的名称，以及后续的建立进化树的步骤中，往往需要名字的替换，并建立相应的矩阵，并以此作为基础推断物种之间的进化关系。在分子生物地理学和进化生态学中，这种需求更为迫切。为了更为方便得分析处理DNA-Barcoding所得的序列，方便得更改名称，处理比对后的各序列拼接成一致性的矩阵等，必须开发相应的软件。

有鉴于此，本人利用开源的R语言开发了phylotools软件包。其中的函数均为笔者在处理DNA-Barcoding数据时用到的函数。现在已经上传到R的CRAN网站。全部源代码及多种平台上的程序包都可以在CRAN上获得。网址为

http://cran.r-project.org/web/packages/phylotools/index.html

下面简要介绍一下各函数的主要功能，供业界的同行参考：

  • complement() 给出给定DNA序列的反向互补序列，输入格式为字符串。
  • fasta.split() 给出各名称分组的对照表，将给定的fasta文件分割成几个独立的fasta文件
  • phy2dat() 将phylip文件转换成相应的数据框，以便进行相应的处理
  • read.phylip() 读取序列比对好之后的phylip文件
  • rename.fasta() 为fasta对象中的序列改名。
  • reverse() 给出该序列的反向序列
  • seq2fasta() 将seq文件（一般是 SeqMAN生成）转换成fasta文件
  • sub.tip.label() 给出各名称的对照表，将进化树末端的名称替换。
  • supermat() 基于指定的phy文件构建多个基因的超级矩阵
  • uniquefasta() 将fasta文件中名称重复的序列删除。
  • write.mat() 将建立好的超级矩阵保存在本地硬盘上。

当然，还有很多功能需要进一步实现，如在GenBank上检索并下载DNA序列等等。如您在使用过程中发现程序中的任何错误，欢迎发邮件及时告知。

如何计算两日期相差的天数？

今天讲的日期是公历日期，农历日期由于涉及到朔望月等较为高深的内容，暂时已经超出了本人的能力范围，故先不探讨。

现行的公历随月份及年份天数不同，如何计算两个日期之间相隔多少天？

这里，介绍一种天文上常用的儒略日，并介绍儒略日与公历的相互转换方法，附上相应的R语言程序。

儒略日是天文上常用的一种计时方法，从公元前4713年1月1日格林尼治平太阳间正午12点开始，每增加一天，儒略日增加1，一直向下累加。(以下内容改写自维基百科)

儒略日是法国学者Joseph Justus Scliger（1540-1609）为纪念他的父亲Julius Caesar Scaliger（1484-1558）在1583年提出来的。 　　
儒略日的起点确定考虑了太阳、月亮的运行周期，以及古罗马税收的间隔。

Joseph Scliger定义儒略周期为7980年，是因28、19、15的最小公倍数，28×19×15=7980。
其中：

  • 28年为一太阳周期(solar cycle)，经过一太阳周期，则星期的日序与月的日序会重复。 　　

  • 19年为一太阴周期，或称默冬章(Metonic cycle)，因235朔望月=19回归年，经过一太阴周期则阴历月年的日序重复。

  • 15年为一小纪(indiction cycle)，此为罗马皇帝君士坦丁（Constantine）所颁，每15年评定财产价值以供课税，是古罗马用的一个纪元单位，故以7980年为一儒略周期，而所选的起点公元前4713年，则是这三个循环周期同时开始的最近年份。

在中国科学院紫金山天文台编纂的《中国天文年历》上，有相应年份逐日的儒略日表，可供参考。

还是回到原来的问题，如何计算公历中两个日期相差的天数？办法之一，就是将二者都转换成儒略日，计算其差值。实际上，天文学家也是依靠儒略日来计算天体动态的。

下面是已知日期计算儒略日和已知儒略日计算日期的方法。用R语言写成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
### 已知日期计算儒略日
### y 年 m 月 d日

date2jd <- function(y,m,d){
   n=0
   G=0
   if(y*372+m*31+floor(d)>=588829){
   G=1
   }
   if(m<=2) {
   m = m +12
   y = y -1
   }

   if(G) {
   n=floor(y/100)
   n=2-n+floor(n/4)
   }

   res <- floor(365.25*(y+4716)) + floor(30.6001*(m+1)) + d + n - 1524.5
   return(res)
}

### 已知儒略日，计算日期的公式
###

jd2date <- function(jd){
    ### 转换日期格式
    ### 已知儒略日，用jd2date求得到日期，变为年，月，日
    jdate2vect <- function(xxx){
        year = xxx[[1]]
        month = xxx[[2]]
        day <- xxx[[3]]
        frac <- xxx[[6]]/(60*60*24)+xxx[[5]]/(60*24)+xxx[[4]]/24
        day.dec <- day + frac
        res <- c(year, month, day.dec)
        names(res) <- c("Year","Month","Day")
        return(res)
    }

   D = floor(jd+0.5)
   F= jd+0.5-D
   if(D>=2299161) {
      c = floor((D-1867216.25)/36524.25)
      D = D + 1+c-floor(c/4);
   }

   D = D + 1524;              
   r.Y = floor((D-122.1)/365.25);
   D = D - floor(365.25*r.Y);  
   r.M = floor(D/30.601);
   D = D- floor(30.601*r.M);  
   r.D = D;

   if(r.M>13){
      r.M=r.M - 13
      r.Y=r.Y  - 4715;
   }else{
      r.M =r.M - 1
      r.Y = r.Y- 4716
   }
   F= F*24;
   r.h=floor(F);
   F= F -r.h;
   F = F * 60;
   r.m=floor(F);
   F= F - r.m;
   F = F * 60;
   r.s=F;
   res <- list(r.Y, r.M, r.D, r.h, r.m, round(r.s,2))
   names(res) <- c("Year","Month","Day","Hour","Minute","Second")
   return(jdate2vect(res));

  }

使用方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# ## date2jd 举例
# 
# ## 求2010年9月21日与1980年1月1日相差的天数
date2jd(2010,9,21) - date2jd(1980,1,1)
# 结果：11221天
# 
# ## 求2035年9月2日北京日全食距离现在的天数
date2jd(2035,9,2) - date2jd(2010,9,21)
# 结果：9112天
# 
# ## 求美国独立距离现在的天数
date2jd(2010,9,21) - date2jd(1776,7,4)
# 结果：85545天

# ## 求公元前841年1月1日（西周共和元年）距离现在的天数
date2jd(2010,9,21) - date2jd(-841,1,1)
# 结果：1041578 天

# ## 儒略日转年月日举例
# #已知儒略日为2455230.5，求其对应的公历日期。
jd2date(2455230.5)
# 
# 结果：
#  Year Month   Day
#  2010     2     3
#  是2010年2月3日。

NotePad++:记事本的替代程序

Notepad++是开源的文本程序，是用C++编写的。目前只能在Windows上运行。NotePad++是小巧的编辑器，最新版本5.7.1的安装文件仅为3.88M. 但是其功能确是十分强大的，占用系统资源很低而运行速度很快。

这个软件的特点，这里简要介绍一下：

首先，NotePad++支持几十种编程语言的高亮显示，如著名的C,C++,C#, Fortran, Java, Python, Perl, SQL, shell, PHP, javascript，Html, TeX等等。初次接触NotePad++是2009年5月。当时正准备找一个R程序脚本的编辑器，很多人推荐用TinnR,但是TinnR虽然具有R的语法高亮功能，但是编辑风格与记事本有较大不同，我很难适应其风格。后来看到论坛上有人介绍NotePad++与NppToR,不但能实现R的语法高亮功能，也能可以一键将当前脚本输送到R-console中。小巧的软件，完备的功能让人兴奋不已。应大量用户的要求，NotePad++新近增加了R语言的高亮显示，使得R用户能方便得编写R的脚本及程序。

NotePad++的TextFX具有出色的文本编辑和转换功能。TextFX是嵌入到NotePad++中的模块之一，能够十分方便的进行文本的大小写的转换，行转换，编码的转换，删除空白行，删除多余的空格等等，并且支持正则表达式。

NotePad++ 的Plugins具有扩展功能。其中Aspell模块具有检查拼写的功能，配合GNU的aspell软件，能将拼写错误的单词及时找出，并依据用户的选择作出相应的替换。NppExport能够将高亮显示的结果导出成rtf, html等多种格式。Compare模块可以比较两个文件的异同。如果对新版本的程序进行了修改，想知道修改在哪些地方，又不想用庞大的svn软件，Notepad++是一个不错的选择。

当然，NotePad++还有记录Macro的功能，同时搜寻打开的所有文件中的某一字段功能等，在此不一一列举了。

如果你还没有试过NotePad++，那么可以先试一试，估计大多数人，即使不是程序员，都会喜欢上这个小巧灵活，功能强大的软件。

NotePad++的地址
http://notepad-plus-plus.org/

R语言：行星运行轨迹的绘制

前一篇文章中介绍了如何用R绘制行星的周年视运动，这一则介绍如何绘制行星在一段时间的运行轨迹。我对R的moonsun 程序包（参见 http://ftp.ctex.org/mirrors/CRAN/web/packages/moonsun/index.html） 进行了修改，增加了一个track函数，以绘制任意一段时间内的行星在星空背景上的运行轨迹。

废话少说，先上几张图吧

img

图1 2010年9月22日-12月30日 木星在星空背景的运行轨迹

img

图2 2010年8月3日-12月7日 火星在星空背景的运行轨迹

img

图3 2010年1月1日-12月31日 水星的视运动
img

图4 2010年7月30日 - 9月27日 水星在星空背景上的移动

img

图5 2011年9月22日 - 2011年12月30日 土星在星空背景上的移动

img

图6 2008年8月1日 - 2008年11月8日 天王星在星空背景上的移动

img

图7 2011年4月30日- 2011年8月7日 金星在星空背景上的移动

感兴趣的读者可以下载最新的moonsun程序包，

我对该程序包进行了重新编译

源代码 和Windows版本的程序

下载

基础天文计算的moonsun程序包